Wir brechen jetzt schon 1,5 Grad! Wenn das so weitergeht, werden wir bald 2, dann 3 Grad Erwärmung haben. Das wäre ein Ende der Zivilisation, wie wir sie kennen. Das sind reine Messungen, keine Ideologie.
Der Statistiker Grant Foster hat fünf Datensätze zusammengefasst und kam zu einem neuen Ergebnis. Er schreibt: Bereits im Jahr 2011 habe ich zusammen mit Stefan Rahmstorf (Foster & Rahmstorf 2011, im Folgenden FR11) einen Artikel verfasst, in dem wir die globale Temperatur angepasst haben, um (so gut wir konnten) den Einfluss von Faktoren zu beseitigen, von denen wir wussten, dass sie nur vorübergehend waren und nicht menschengemacht. Konkret handelt es sich dabei um Vulkanausbrüche (deren Aerosole den Planeten abkühlen), die El-Niño-Südoszillation (ENSO, die die Welt in ihrer positiven El-Niño-Phase erwärmt und in ihrer negativen La-Niña-Phase abkühlt) und Sonnenschwankungen (wenn die Sonne heißer oder kälter ist, so auch die die Erde). Diese exogenen Faktoren führen dazu, dass die globale Temperatur schwankt, aber nicht wirklich etwas bewirkt; durch die Beseitigung ihres Einflusses wird der Teil der globalen Erwärmung klarer.
Ich habe meine Methode hierfür aktualisiert und den Zeitraum, den sie abdeckt, erweitert, daher möchte ich einige der Änderungen an der Methodik mit Ihnen teilen. Aber bevor ich das tue, komme ich gleich auf den Punkt. Es werden viele Schwankungen der globalen Temperatur entfernt, so dass die jährlichen Durchschnittswerte seit 1950 für fünf wichtige globale Temperaturdatensätze wie folgt aussehen:
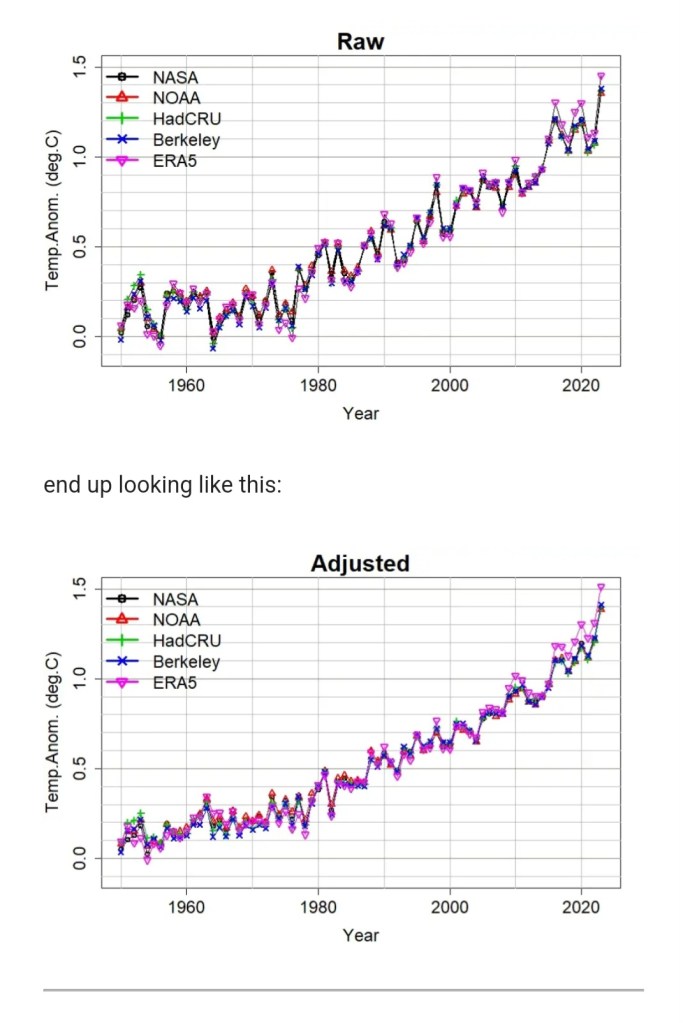
Quelle: Open Mind von Grant Foster
Es gibt drei wesentliche Änderungen in der Methodik. Erstens geht es um die Verwendung neuer Datensätze.
1. Für vulkanische Aerosole habe ich die für CMIP6-Modellläufe verwendeten Daten erfasst, die viel aktueller sind als die Daten, die wir in FR11 verwendet haben. Für ENSO verwende ich den Soutern Oscillation Index (SOI) anstelle des Multivariate El Niño Index (MEI). Für die Sonneneinstrahlung verwende ich die Sonnenfleckenzahlen als Stellvertreter.
2. Zweitens verwende ich keine verzögerte Regression mehr (d. h. die Temperatur wird anhand verzögerter Versionen der Daten für Vulkan-, El-Niño- und Sonneneinflüsse regressiert und die Verzögerungen werden nach der Methode der kleinsten Quadrate ausgewählt), stattdessen glätte ich die Daten exponentiell und regressiere dagegen geglättete Versionen (Auswahl der Glättungszeitskalen nach der Methode der kleinsten Quadrate).
3. Drittens modelliere ich den Teil des Signals „globale Erwärmung“ nicht mehr mit einer geraden Linie. Das war für FR11 in Ordnung, denn im betreffenden Zeitraum (1979 bis 2010) folgte es einer geraden Linie (tatsächlich sehr genau). Aber die neue Zeitspanne beginnt im Jahr 1950, und seitdem ist der Teil des Signals zur globalen Erwärmung um einiges komplizierter als eine gerade Linie; Jetzt modelliere ich es als allgemeine Funktion der Zeit g(t), die durch eine Lowess Smooth geschätzt wird. Daher ist das Modell jetzt
x(t) = g(t) + c_v V_j(t) + c_S S_k(t) + c_R R_l(t) + \varepsilon(t),
Dabei ist g(t) eine generische Funktion der Zeit (hauptsächlich vom Menschen verursachte globale Erwärmung), Vj(t) die exponentiell geglättete optische Tiefe des Vulkanaerosols auf einer Zeitskala von j Monaten, Sk(t) der exponentiell wirkende Southern Oscillation Index SOI geglättet auf einer Zeitskala von k Monaten, Rl(t) ist die exponentiell geglättete Sonnenfleckenzahl auf einer Zeitskala von l Monaten, und \varepsilon(t) ist ein stationärer Rauschprozess. Die Funktion g(t) wird durch eine Lowess Smooth bestimmt, die Koeffizienten cj, ck und cl und die Zeitskalen j, k und l werden durch die Methode der kleinsten Quadrate bestimmt. Durch deren Kombination entsteht ein verallgemeinertes additives Modell.
Die erste Iteration des Prozesses besteht darin, eine glatte Kurve an die Daten x(t) anzupassen, um die Funktion g(t) anzunähern. Dies wird von den Daten abgezogen und die Vulkan-, El-Niño- und Sonnenfaktoren (und ihre Glättungszeitskalen) werden nach der Methode der kleinsten Quadrate an diese Residuen angepasst. Subtrahiert man diese letzte Anpassung von den Originaldaten, bleiben angepasste Daten übrig.
Für die zweite Iteration wird eine glatte Kurve an die angepassten Daten aus Iteration 1 angepasst, die neue glatte Kurve wird von den Originaldaten subtrahiert und exogene Faktoren werden daran angepasst. Dies ist der Prozess der Nachanpassung, der die Tatsache kompensieren soll, dass die ursprüngliche glatte Oberfläche einen Teil des exogenen Einflusses entfernt hat, noch bevor wir sie mit der Methode der kleinsten Quadrate anpassen. Die Anpassung der zweiten Iteration an die exogenen Faktoren stimmt daher besser überein.
Und der Vorgang kann wiederholt werden, bis er der besten Näherung entspricht (sogenanntes Projection Pursuit). In diesem Fall stellte ich fest, dass fünf Iterationen (d. h. vier Iterationen der Nachanpassung) mit ausreichender Präzision konvergierten.
Die Details und Übersichten dazu kann man hier weiterlesen: https://tamino.wordpress.com/2024/02/16/adjusted-global-temperature-data/
Source / Posted on February 16, 2024 in Open Mind

